Mathematics
William Paul Thurston: “Mathematics is not about numbers, equations, computations or algorithms: it is about understanding.”
Meet the Mathematics Department
|
Name: |
Title: |
Email address: |
|
Mr S. Hodgson |
Head of Department |
|
|
Mr S. Horne |
Second in Department |
|
|
Mrs R. Hall |
Teacher of Mathematics |
|
|
Mr J. Grayston |
Teacher of Mathematics |
|
|
Mr J. Seggie |
Teacher of Mathematics |
|
|
Ms V. Horrocks |
Head of Year, Teacher of Mathematics & PE |
|
|
Mr R. Specterman |
Teacher of Mathematics |
|
|
Mr C. Lovell |
Teacher of Mathematics |
|
|
Mr W. McKee |
Teacher of Mathematics |
|
|
Miss T. Ellis |
Maths tutor Intervention |
Intent
Our curriculum is firmly based within the Teaching for Mastery principles of the NCETM and their “Five Big Ideas”, namely coherence, representation and structure, mathematical understanding, variation and fluency.
Coherence
In order to build up concepts in a highly detailed, secure and deep way, key ideas are broken down into constituent atoms that are then explained, modelled and practiced independently over time. In order to secure ever greater understanding and ever more complex schema, these atoms are then developed over time, each time ensuring that students generate the answers to questions through independent practice. Topics are focussed on in detail for a significant amount of time. Rather than spiralling through a variety of topics each year, individual topics are looked at in depth, ensuring students encounter mathematical ideas in a number of different forms, and look at understanding these mathematical ideas using a number of different representations and analogies.
Representation and structure
The use of analogy, both visual and verbal, is an important way of ensuring students build a robust understanding of the underlying structure of mathematics. As such, our curriculum ensures that graphical representation are used where possible (for example using bar modelling for solving equations or diagrammatic examples for any work with fractions.) Links to analogies that are clearly interpretable by students, such as using the examples of car colours for estimates of frequency, allows students a way in to understanding complex concepts by clear representation.
Mathematical understanding
The aim of the curriculum is to secure a deep understanding or mathematical principles, dispensing with quick win algorithmic tricks in favour of spending a significant amount of time looking at mathematical ideas in significant detail. A strong focus is put on mathematical literacy, with key words used and insisted on throughout the curriculum. Representations are also used as a key way to elucidate understanding in topics that can often be reduced to algorithmic procedures (such as expanding single brackets, or multiplying fractions.)
Fluency
Fluency is a critical requirement for students to progress mathematically, either in terms of progressing skills in terms of complexity or in terms of moving on to complex mathematical problem solving. In order to develop fluency, significant levels of independent practice is insisted upon. These techniques are clearly and carefully modelled by staff.
Variation
When activities are used to develop fluency, opportunities are sought to use variation for a number of purposes. This can be in order to show a range of ideas in a subject to help students understand a breadth of techniques and not develop misconceptions (such as in the case of the placement of the unknown when solving equations), or in order to use increasingly difficult questions as a form of differentiation that still ensures all students are working on the same “atom.”
Our Year 7 curriculum provides a solid foundation in number and the beginning of algebra, before closing out with fraction to crossover between number and proportion. In year 8 they study proportion until Christmas, looking deeply at ratio and percentages. After this, they study algebra for the remainder of the year, looking at a variety of topics and techniques from expanding brackets, through solving equations and ending with looking at drawing graphs (forming a crossover topic with the applied mathematics of year 9.) Year 9 sees them apply their knowledge of number and algebra to statistics, probability and geometry.
After this the students are set ready for their GCSE studies. Year 10 foundation studies study the AQA GCSE maths specification, where they strengthen their knowledge of previous 
content as well as looking in detail at examination questions and techniques for answering them. Higher students further their studies into higher level topics in algebra, statistics, probability, number, proportion and geometry.
Maths is embedded as a subject not only about its own internal disciplinary language, techniques and purpose but also as a subject that exists beyond the walls of the classroom. Regular discussion of careers in mathematics, and historical mathematical figures from diverse backgrounds are undertaken, and students are shown in what circumstances and by whom key mathematical techniques are used.
Scheme of Learning/Courses/Curriculum Map
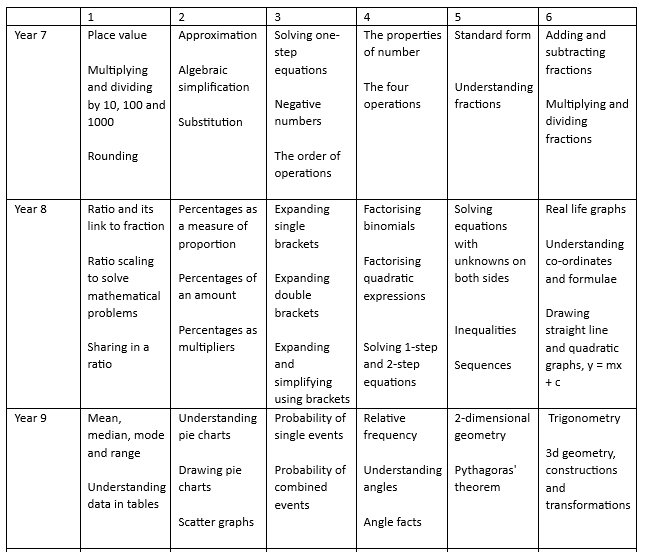
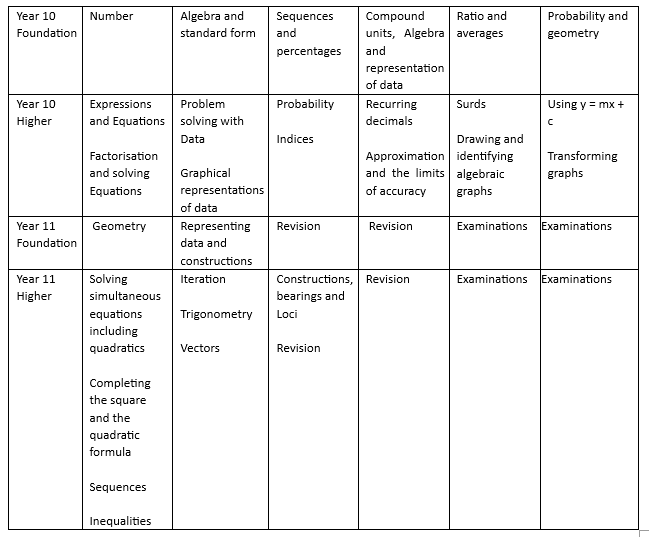
Exam Board Specification - AQA GCSE Mathematics
https://www.aqa.org.uk/subjects/mathematics/gcse/mathematics-8300/specification-at-a-glance
Feedback Policy
The primary purpose of feedback is to move students on with their learning. Students receive feedback on their learning in a number of different ways, both formally and informally.
Formative assessment takes place every lesson in many forms including:
- Low stakes quizzing
- Like marking in lessons
- Questioning
- Peer and self-assessment (green pen)
- Examination style questions
Students are provided with detailed written feedback on longer pieces of written work and key pieces. Next steps marking is implemented, alongside other techniques to promote learning and progress. Students are expected to respond to their feedback and make improvements to their work by acting upon it immediately using purple pen.